I decided to migrate my academic website from WordPress to Jekyll. You can find the new website at https://maguilera.net/
I’m happy to share that I started to work on a new project funded by a MSCA-IF grant to work at the University of Sussex in collaboration with Chris Buckley.
The project aims to apply information-theoretic and inference methods to develop models of neural activity from zebrafish larvae in closed look behavior, e.g. trying to apply theoretical methods for approximating the behaviour of very large networks and inferring their parameters from experimental data.
Project description
A major challenge in cognitive neuroscience is to understand how behaviour arises from the dynamical interaction of an organism’s nervous system, its body, and its environment. Understanding embodied neural activity involves the resolution of various conceptual, technical and methodological issues in explaining how living organisms self-organize at many levels (from neural bio-chemistry to behaviour and learning). Currently, two important obstacles hinder this endeavour: the difficulties in recording neural activity in behaving animals, and the lack of mathematical tools to characterize the complex brain-body-environment interactions in living organisms. In this project we will address current limits by implementing an interdisciplinary combination of novel animal behaviour neuroimaging setups and large-scale statistical methods, with the goal of recording and modelling whole-brain activity of locomoting vertebrates. We will study fictively swimming larval zebrafish during active behaviour in a pioneering experimental setup, recording neural activity utilizing light-sheet microscopy for calcium imaging in different virtual reality scenarios involving sensorimotor manipulations. In this setup, we will collect data from the distributed neural circuits that integrate sensory signals from the environment (exafferent input) and their own movements (reafferent input), as well as plastic processes of habituation to new sensorimotor contingencies. From this data, we will infer large-scale generative models (i.e. models capable of yielding synthetic data resembling the studied phenomena) of embodied neural circuits by complementing dynamical models and techniques from statistical mechanics with innovative information theoretic and Bayesian inference methods and approximations for very large systems in non-equilibrium and non-stationary conditions.
I just published a new paper exploring some of the ideas we initiated in our Integrated information in the thermodynamic limit (Aguilera & Di Paolo, 2019) paper. Here, I explore in detail many of the assumptions of Integrated Information Theory (specifically IIT 3.0) by computing integration in large kinetic Ising networks presenting a critical point. By combining a simple model with tractable statistical properties that can be analytically characterized with architectures, I show that some assumptions in the theory are problematic for capturing some of the properties associated with critical phase transitions. This example compels researchers interested in IIT and related indices of complexity to apply such measures under careful examination of their design assumptions. Rather than applying the measure off-the-shelf, this work offers some methods to explore in more depth the assumptions behind the measure and how it applies to each situation
Aguilera, M & Di Paolo, EA (2019). Scaling Behaviour and Critical Phase Transitions in Integrated Information Theory. Entropy 2019, 21(12), 1198; https://doi.org/10.3390/e21121198
Abstract: Integrated Information Theory proposes a measure of conscious activity (Φ), characterised as the irreducibility of a dynamical system to the sum of its components. Due to its computational cost, current versions of the theory (IIT 3.0) are difficult to apply to systems larger than a dozen units, and, in general, it is not well known how integrated information scales as systems grow larger in size. In this article, we propose to study the scaling behaviour of integrated information in a simple model of a critical phase transition: an infinite-range kinetic Ising model. In this model, we assume a homogeneous distribution of couplings to simplify the computation of integrated information. This simplified model allows us to critically review some of the design assumptions behind the measure and connect its properties with well-known phenomena in phase transitions in statistical mechanics. As a result, we point to some aspects of the mathematical definitions of IIT 3.0 that fail to capture critical phase transitions and propose a reformulation of the assumptions made by integrated information measures.
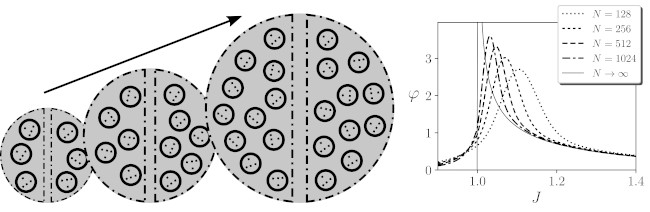
Together with Ezequiel Di Paolo, we have just published a new paper in which we explore how integrated information scales in very large systems. The capacity to integrate information is crucial for biological, neural and cognitive processes and it is regarded by Integrated Information Theory (IIT) proponents as a measure of conscious activity. In this paper we compute (analytically and numerically) the value of IIT measures (φ) for a family of Ising models of infinite size. This is exciting since it allows to explore situations that were very far to the kind of systems that can be generally analyzed in IIT, generally limited to a few units due to its computational cost. Moreover, our analysis allows us to connect features of integrated information with well-known features of critical phase transitions in statistical mechanics.
Aguilera, M & Di Paolo, EA (2019). Integrated information in the thermodynamic limit. Neural Networks, Volume 114, June 2019, Pages 136-146. doi:10.1016/j.neunet.2019.03.001
Abstract: The capacity to integrate information is a prominent feature of biological, neural, and cognitive processes. Integrated Information Theory (IIT) provides mathematical tools for quantifying the level of integration in a system, but its computational cost generally precludes applications beyond relatively small models. In consequence, it is not yet well understood how integration scales up with the size of a system or with different temporal scales of activity, nor how a system maintains integration as it interacts with its environment. After revising some assumptions of the theory, we show for the first time how modified measures of information integration scale when a neural network becomes very large. Using kinetic Ising models and mean-field approximations, we show that information integration diverges in the thermodynamic limit at certain critical points. Moreover, by comparing different divergent tendencies of blocks that make up a system at these critical points, we can use information integration to delimit the boundary between an integrated unit and its environment. Finally, we present a model that adaptively maintains its integration despite changes in its environment by generating a critical surface where its integrity is preserved. We argue that the exploration of integrated information for these limit cases helps in addressing a variety of poorly understood questions about the organization of biological, neural, and cognitive systems
I just published with Manuel Bedia a paper in Scientific Reports that results from an exploration of how tools from statistical mechanics could be used to model adaptive mechanisms. In this paper, we explore how adaptation to criticality could be used as a general adaptive mechanism in robots controlled by a neural network, using a simple mechanism that preserves a specific structure of correlations. This has interesting implications for thinking about neural and cognitive systems, which instead of relying on internal representations about an external world could adapt by preserving a complex structure of internal correlations.
Aguilera, M & Bedia, MG (2018). Adaptation to criticality through organizational invariance in embodied agents. Scientific Reports volume 8, Article number: 7723 (2018). doi:10.1038/s41598-018-25925-4
Abstract: Many biological and cognitive systems do not operate deep within one or other regime of activity. Instead, they are poised at critical points located at phase transitions in their parameter space. The pervasiveness of criticality suggests that there may be general principles inducing this behaviour, yet there is no well-founded theory for understanding how criticality is generated at a wide span of levels and contexts. In order to explore how criticality might emerge from general adaptive mechanisms, we propose a simple learning rule that maintains an internal organizational structure from a specific family of systems at criticality. We implement the mechanism in artificial embodied agents controlled by a neural network maintaining a correlation structure randomly sampled from an Ising model at critical temperature. Agents are evaluated in two classical reinforcement learning scenarios: the Mountain Car and the Acrobot double pendulum. In both cases the neural controller appears to reach a point of criticality, which coincides with a transition point between two regimes of the agent’s behaviour. These results suggest that adaptation to criticality could be used as a general adaptive mechanism in some circumstances, providing an alternative explanation for the pervasive presence of criticality in biological and cognitive systems.
I have recently published a new paper where we model social coordination in self-organized crowds social media, using data from the 15M movement in Spain:
Crowd behaviour challenges our fundamental understanding of social phenomena. Involving complex interactions between multiple temporal and spatial scales of activity, its governing mechanisms defy conventional analysis. Using 1.5 million Twitter messages from the 15M movement in Spain as an example of multitudinous self-organization, we describe the coordination dynamics of the system measuring phase-locking statistics at different frequencies using wavelet transforms, identifying 8 frequency bands of entrained oscillations between 15 geographical nodes. Then we apply maximum entropy inference methods to describe Ising models capturing transient synchrony in our data at each frequency band. The models show that all frequency bands of the system operate near critical points of their parameter space and while fast frequencies present only a few metastable states displaying all-or-none synchronization, slow frequencies present a diversity of metastable states of partial synchronization. Furthermore, describing the state at each frequency band using the energy of the corresponding Ising model, we compute transfer entropy to characterize cross-scale interactions between frequency bands, showing a cascade of upward information flows in which each frequency band influences its contiguous slower bands and downward information flows where slow frequencies modulate distant fast frequencies.
I recently started at a new postdoc position in the IAS Research Centre for Life, Mind and Society at the University of the Basque Country, funded by a postdoc grant from this university.
I will be working with Ezequiel Di Paolo in my postdoc project ‘Information Theory and Maximum Entropy Modelling in Embodied Organisms’.
This paper is an extension of some of the results worked during my PhD thesis. We investigate how the source of metastability in cognitive activity is not necessarily restricted to the action of neural circuits alone, but in some circumstances it can be generated from the sensorimotor coupling between an agent’s brain and its environment.
Aguilera M, Bedia MG and Barandiaran XE (2016) Extended Neural Metastability in an Embodied Model of Sensorimotor Coupling. Frontiers in Systems Neuroscience 10:76. doi: 10.3389/fnsys.2016.00076
Using a robotic simulated agent and information theoretical tools we are able to show how (1) the bidirectional coupling between agent and environment brings the system closer to a regime of criticality and triggers the emergence of additional metastable states which are not found in the brain in isolation but extended to the whole system of sensorimotor interaction, (2) the synaptic plasticity of the agent is fundamental to sustain open structures in the neural controller of the agent flexibly engaging and disengaging different behavioral patterns that sustain sensorimotor metastable states, and (3) these extended metastable states emerge when the agent generates an asymmetrical circular loop of causal interaction with its environment, in which the agent responds to variability of the environment at fast timescales while acting over the environment at slow timescales, suggesting the constitution of the agent as an autonomous entity actively modulating its sensorimotor coupling with the world.
Last week I defended my PhD dissertation entitled ‘Interaction Dynamics and Autonomy in Cognitive Systems’. It was a beautiful and intense experience for closing four years of work. The thesis was examined by Ricard Solé, Ezequiel di Paolo and Seth Bullock, which provided several points of discussion for a rich and stimulating debate about the contributions of the dissertation and lines of further development.
I should thank Manuel Bedia, Xabier Barandiaran and Francisco Serón for their extraordinary work as supervisors and collaborators, as well as many other people that has supported the work developed in this dissertation.
The complete dissertation can be freely downloaded from here:
Also, you can check the slides of the presentation
Some time ago I published a paper with Arnau Monterde, Antonio Calleja-López, Xabier Barandiaran y John Postill about collective identities in the 15M and related networked movements. We argue that the 15M movement in Spain demands conceptual and methodological innovations. Its rapid emergence, endurance, diversity, multifaceted development and adaptive capacity, posit numerous theoretical and methodological challenges. We show how the use of structural and dynamic analysis of interaction networks (in combination with qualitative data) is a valuable tool to track the shape and change of what we term the ‘systemic dimension’ of collective identities in network-movements. We show how the 15M movement displays a specific form of systemic collective identity we call ‘multitudinous identity’ , characterized by social transversality and internal heterogeneity, as well as a transient and distributed leadership driven by action initiatives. Our approach attends to the role of distributed interaction and transient leadership at a mesoscale level of organizational dynamics, which may contribute to contemporary discussions of collective identity in network-movements.
Monterde, A., Calleja-López, A., Aguilera, M., Barandiaran, X. E., & Postill, J. (2015). Multitudinous identities: a qualitative and network analysis of the 15M collective identity. Information, Communication and Society, doi: 10.1080/1369118X.2015.1043315
Miguel Aguilera's academic website (old) 